KRISTALLSYSTEME UND BRAVAIS-GITTER
Kristallsysteme bieten ein symmetriebezogenes Klassifizierungsschema für kristalline Festkörper. In der Kristallographie werden die zu beschreibenden Kristalle mit Hilfe des Kristallsystems dreidimensional klassifiziert. Es gibt sieben verschiedene Kristallsysteme: kubisch, hexagonal, tetragonal, trigonal, orthorhombisch, monoklin und triklin.
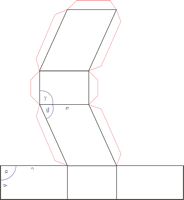
Ein Bravais-Gitter (nach dem französischen Physiker Auguste Bravais) ist ein unendliches Gitter von Raumpunkten mit einer Anordnung und Orientierung, die exakt gleich aussieht, egal von welchem Gitterpunkt wir das Gitter betrachten. Ein Kristallgitter durch Angabe des Bravais-Gitter und der Anordnung der Atome in der zugehörigen Einheitszelle bestimmt. Es gibt 14 Bravais-Gitter: 7 primitive Gitter mit einem Gitter-punkt pro Einheitszelle und 7 zentrierte Gitter mit mehreren Gitterpunkten pro Einheitszelle.
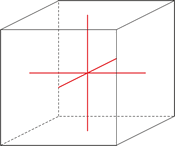
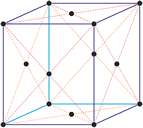
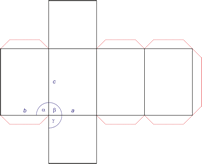
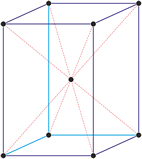
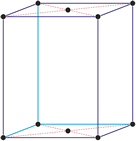
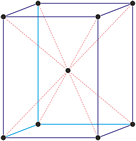
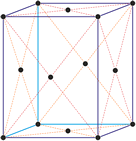
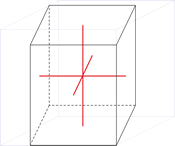
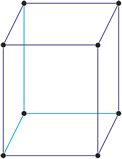
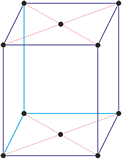
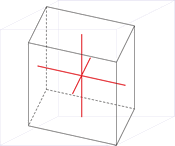
Kubisches Kristallsystem
Im kubischen Kristallsystem (isometrischen Kristallsystem) alle drei Achsen des Achsenkreuzes sind gleich lang und schneiden sich im rechten Winkel.
a = b = c
α = β = γ = 90°
primitiv (cP)
raumzentriert (cI)
flächenzentriert (cF)
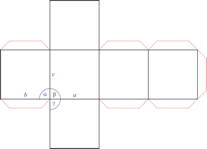
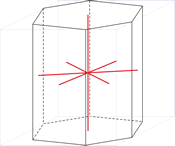
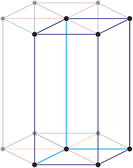
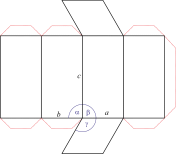
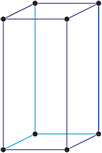
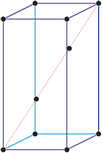
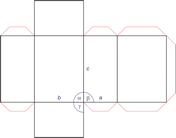
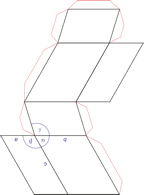
Hexagonales Kristallsystem
Eine hexagonale Einheitszelle hat vier Achsen. Drei gleich lange Achsen (bezeichnet mit a1, a2 und a3) auf einer Ebene die sich unter 120° schneiden. Eine vierte Achse (c), die länger oder kürzer sein kann steht senkrecht zu dieser Ebene.
Die Parameter der Einheitszelle sind:
a = b ≠ c
α = β = 90° γ = 120°
Das Volumen der hexagonalen Einheitszelle gegeben durch
primitiv (hP)
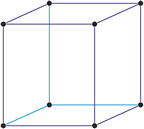
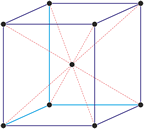
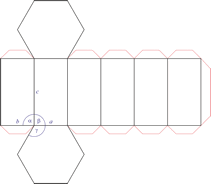
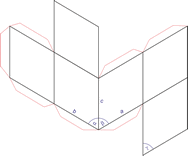
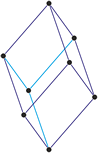
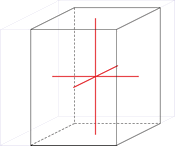
Trigonales Kristallsystem
Ein trigonales Kristallsystem ist ein Kristallsystem, dessen Elementarzelle die gleichen Kantenlängen aufweist. Die drei Winkel sind ebenfalls gleich groß, jedoch nicht rechtwinkelig. Ein Rhomboeder lässt sich aus einem Würfel durch Deformation senkrecht zu einer der Raumdiagonalen ableiten.
a = b = c
α = β = γ ≠ 90°
Bezogen auf rhomboedrische Achsen
Bezogen auf hexagonale Achsen
primitive hexagonalen Gitter (hP)
primitive rhomboedrische Gitter (hR)
Rhomboedrische Gitter können ebenfalls im hexagonalen Gitter beschrieben werden:
a = b ≠ c
α = γ = 90° β = 120°
R-zentrierte hexagonalen Gitter (hR)
Abbildung zeigt die rhomboedrische primitiven Zelle in hexagonaler Aufstellung
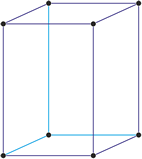
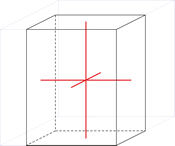
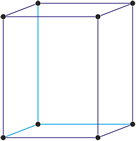
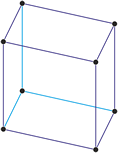
Tetragonales Kristallsystem
Im tetragonalen Kristallsystem zwei Achsen des Achsenkreuzes sind gleich lang, die dritte ist länger oder kürzer. Alle schneiden sich im rechten Winkel.
a = b ≠ c
α = β = γ = 90°
primitiv (tP)
raumzentriert (tI)
Rhombisches Kristallsystem
Im orthorhombischen Kristallsystem (rhombischen Kristallsystem) alle drei Achsen des Achsenkreuzes sind verschieden lang, sie schneiden sich im rechten Winkel.
a ≠ b ≠ c
α = β = γ = 90°
primitiv (oP)
basiszentriert (oC)
raumzentriert (oI)
flächenzentriert (oF)
Monoklines Kristallsystem
Im monoklinen Kristallsystem alle drei Achsen des Achsenkreuzes sind verschieden lang. Zwei davon schneiden sich im rechten Winkel, der Winkel der dritten zu diesen beiden ist beliebig aber ungleich 90 Grad.
a ≠ b ≠ c
α = γ = 90° ≠ β
primitiv (mP)
basiszentriert (mC)
Triklines Kristallsystem
Im triklinen Kristallsystem alle drei Achsen des Achsenkreuzes sind verschieden lang, die Winkel dazwischen sind beliebig, aber ungleich 90 Grad. Das trikline Kristallsystem wird auch als anorthisches Kristallsystem bezeichnet und sein Gittersystem wird daher mit a abgekürzt.
a ≠ b ≠ c
α ≠ β ≠ γ ≠ 90°
primitiv (aP)
Bibliographie:
- International Tables for Crystallography. Volume A: Space-Group Symmetry. ed. Theo Hahn. Published for the International union of crystallography by Springer. Fifth edition, 2005.
- "Online Dictionary of Crystallography." 9 Dec. 2005. IUCr. 28 Apr. 2016. <http://reference.iucr.org/dictionary/Category:Fundamental_crystallography>.
- Cockcroft, Jeremy Karl and Barnes, Paul. "Powder Diffraction on the Web." 1 Feb. 2016. Birkbeck College, University of London. 4 July. 2016. <http://pd.chem.ucl.ac.uk/pd/welcome.htm>.
- Howard, Mike and Howard, Darcy. "Introducción a la Cristalografía y Sistemas Cristalinos." (Traducción al español: Juan José Palafox Reyes; colaborador Porfirio Sosa. Universidad de Sonora, México). Rockhounding Arkansas. 17 June 2016. <http://gaia.geologia.uson.mx/academicos/palafox/index.htm>.
- Infogalactic: the planetary knowledge core contributors. "Trigonal crystal system." 3 Sep. 2015. Infogalactic: the planetary knowledge core. 5 Nov. 2019. <https://infogalactic.com/info/Trigonal_crystal_system>.
Zitieren dieser Seite:
Generalic, Eni. "Kristallsysteme und Bravais-Gitter." EniG. Periodensystem der Elemente. KTF-Split, 25 Nov. 2023. Web. {Datum des Abrufs}. <https://www.periodni.com/de/kristallsysteme-und-bravais-gitter.html>.
