KRISTALNI SUSTAVI I BRAVAISOVE REŠETKE
Kristalni sustav je metoda razvrstanja kristalnih tvari na osnovu njihove jedinične ćelije. Postoji sedam jedinstvenih kristalnih sustava i po redu opadanja simetrije to su: kubični, heksagonski, tetragonski, trigonski, ortorompski, monoklinski i triklinski.
Bravaisova rešetka je beskrajni niz zasebnih točaka čiji se raspored i orijentacija ponavlja iz koje god točke niza se gledalo. Francuski fizičar i kristalograf Auguste Bravais (1811.-1863.) je 1848. godine ustanovio da se u prostoru može konstruirati samo četrnaest različitih prostornih rešetki. Svi kristalni materijali mogu se uklopiti u jedan od ovih rasporeda.
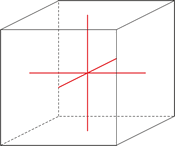
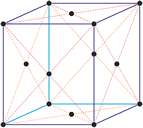
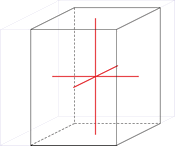
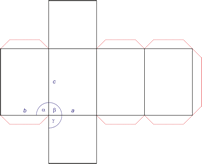
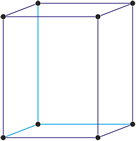
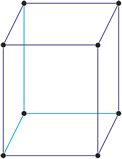
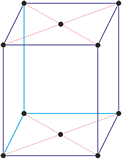
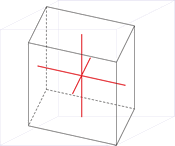
Kubični kristalni sustav
U kubičnom ili teseralnom kristalnom sustavu kristalografske osi jednake su duljine i sijeku se pod pravim kutom.
a = b = c
α = β = γ = 90°
primitivna (cP)
prostorno centrirana (cI)
plošno centrirana (cF)
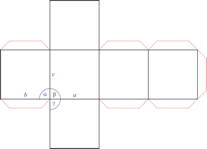
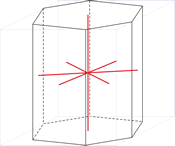
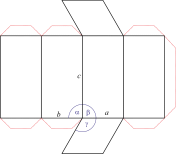
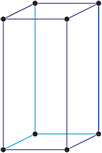
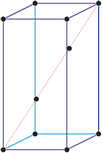
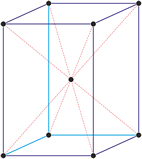
Heksagonski kristalni sustav
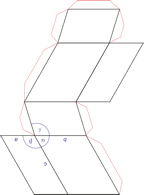
Heksagonski kristalni sustav temeljen je na četiri kristalografske osi. Tri kristalografske osi (označene s a1, a2 i a3) jednake duljine smještene su u jednoj ravnini i međusobno zatvaraju kut od 120° (među svojim pozitivnim krajevima). Četvrta os (c) okomita je na njih i obično je kraća ili duža od ostale tri.
Parametri jedinične ćelije su:
a = b ≠ c
α = β = 90° γ = 120°
Volumen heksagonske jedinične ćelije dan je formulom
primitivna (hP)
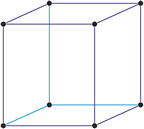
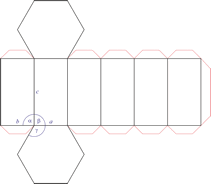
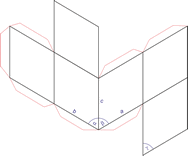
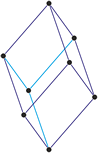
Trigonski kristalni sustav
Trigonski kristalni sustav opisan je s tri primarna vektora jednake duljine koji se sjeku pod jednakim kutovima (≠90°). Trigonska jedinična ćelija izgleda poput kocke koja je istegnuta (ili skraćena) duž jedne prostorne dijagonale.
a = b = c
α = β = γ ≠ 90°
definiran pomoću romboedarskih osi
definiran pomoću heksagonskih osi
primitivna heksagonska rešetka (hP)
primitivna romboedrska rešetka (hR)
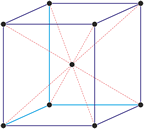
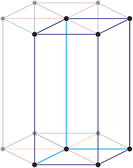
Za opisivanje romboedrske rešetke češće se koristi alternativna jedinična ćelija. Ćelija je istog oblika kao i konvencionalna jedinična ćelija heksagonskog sustava s dvije unutarnje točke jednako razmaknute duž jedne prostorne dijagonale.
a = b ≠ c
α = γ = 90° β = 120°
R-centrirana heksagonska rešetka (hR)
Slika prikazuje odnos romboedarsko-centrirane heksagonske jedinične ćelije i primitivne romboedrske jedinične ćelije
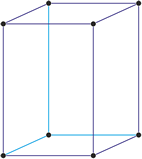
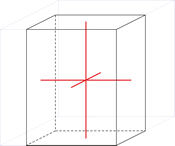
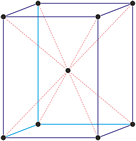
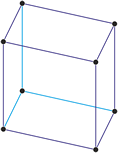
Tetragonski kristalni sustav
U tetragonskom kristalnom sustavu sve tri kristalografske osi okomite su. Dvije vodoravne osi su jednake duljine a treća je duža ili kraća od njih.
a = b ≠ c
α = β = γ = 90°
primitivna (tP)
prostorno centrirana (tI)
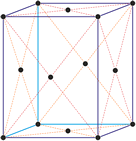
Ortorompski kristalni sustav
U ortorompskom ili rompskom kristalnom sustavu sve su tri kristalografske osi okomite jedna na drugu i različitih duljina.
a ≠ b ≠ c
α = β = γ = 90°
primitivna (oP)
bazno centrirana (oC)
prostorno centrirana (oI)
plošno centrirana (oF)
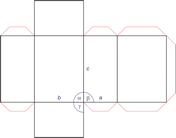
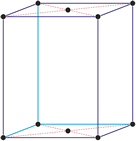
Monoklinski kristalni sustav
U monoklinskom kristalnom sustavu sve tri kristalografske osi različite su duljine. Dvije od njih (a i c) sijeku se pod šiljatim kutom i obično su smještene uspravno. Treća os (b) siječe pod pravim kutom druge dvije osi i naziva se orto os.
a ≠ b ≠ c
α = γ = 90° ≠ β
primitivna (mP)
bazno centrirana (mC)
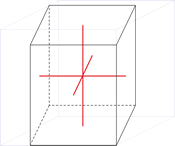
Triklinski kristalni sustav
U triklinskom kristalnom sustavu sve tri kristalografske osi različite su duljine koji međusobno stoje pod kutovima različitim od 90°. Kako niti jedna od triju osi nije okomita na bilo koju drugu os triklinski sustav se ponekad naziva i anortni.
a ≠ b ≠ c
α ≠ β ≠ γ ≠ 90°
primitivna (aP)
Bibliografija:
- International Tables for Crystallography. Volume A: Space-Group Symmetry. ed. Theo Hahn. Published for the International union of crystallography by Springer. Fifth edition, 2005.
- "Online Dictionary of Crystallography." 9 Dec. 2005. IUCr. 28 Apr. 2016. <http://reference.iucr.org/dictionary/Category:Fundamental_crystallography>.
- Cockcroft, Jeremy Karl and Barnes, Paul. "Powder Diffraction on the Web." 1 Feb. 2016. Birkbeck College, University of London. 4 July. 2016. <http://pd.chem.ucl.ac.uk/pd/welcome.htm>.
- Howard, Mike and Howard, Darcy. "Introducción a la Cristalografía y Sistemas Cristalinos." (Traducción al español: Juan José Palafox Reyes; colaborador Porfirio Sosa. Universidad de Sonora, México). Rockhounding Arkansas. 17 June 2016. <http://gaia.geologia.uson.mx/academicos/palafox/index.htm>.
- Infogalactic: the planetary knowledge core contributors. "Trigonal crystal system." 3 Sep. 2015. Infogalactic: the planetary knowledge core. 5 Nov. 2019. <https://infogalactic.com/info/Trigonal_crystal_system>.
Citiranje ove stranice:
Generalić, Eni. "Kristalni sustavi i Bravaisove rešetke." EniG. Periodni sustav elemenata. KTF-Split, 18 Jan. 2024. Web. {Datum pristupa}. <https://www.periodni.com/hr/kristalni-sustavi-i-bravaisove-resetke.html>.
