THE OZONE LAYER IS NOT A SHIELD,
IT IS THE REMNANT OF UV RADIATION PROTECTION

The plunge of photons into the depths of the atmosphere

From the moment it meets the first molecules of atmosphere the light from the Sun changes. By the time they reach the mesopause, photons with a wavelength below 100 nm are almost completely absorbed by atomic oxygen, molecular oxygen and nitrogen. In the middle atmosphere, molecular nitrogen is particularly stable since it cannot be photodissociated below the mesopause. The photochemistry of this part of the atmosphere is dominated by the reactions of oxygen species.

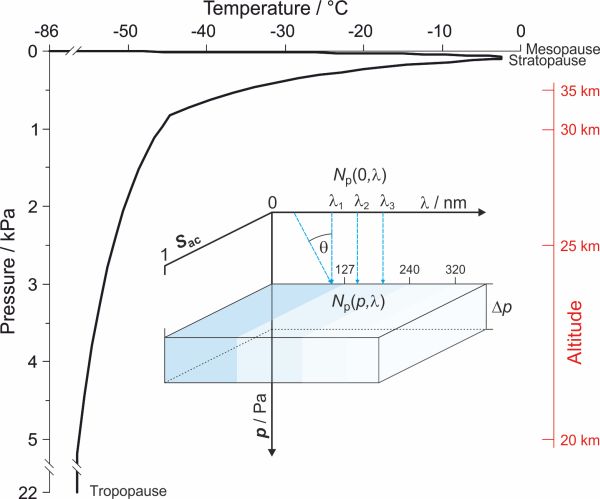
What are the conditions here? As we descend into the depths of the mesosphere the temperature increases from about -86 °C at the top to -2.5 °C at the bottom. After this maximum, the temperature again begins to decrease as we move through the stratosphere to about -56 °C at the tropopause. The pressure increases exponentially with depth, from 0.4 Pa at the mesopause to over 67 Pa at the stratopause and then to 22 631 Pa at the tropopause. Since the density is proportional to the pressure, it also increases exponentially with depth. Figure 3 shows the temperature profile for the 'US standard atmosphere' as a function of pressure.[5]

For a reaction involving the collision of two molecules, the activation energy is the minimum kinetic energy that reactants must have in order to form products. In a gas-phase reaction there are numerous collisions each second, but only a tiny proportion is sufficiently energetic to lead to reaction. The fraction of collisions with a kinetic energy in excess of the activation energy (E_a) is given by the Boltzmann distribution e^-Ea/RT. (Atkins, p.881)

The photochemical paths offer an advantage over the thermal methods of forming thermodynamically disfavored products, as they can overcome large activation barriers in a short period of time and allow reactivity otherwise inaccessible by the thermal methods. We can therefore assume that the ultraviolet parts of the solar radiation are necessary for the initiation of chemical reactions in the middle atmosphere. This assumption is based on the fact that only UV photons can bring enough energy to molecules in the mesosphere and stratosphere so that they, or their fragments, can participate in chemical reactions. With that in mind we will ignore all thermochemical reactions that are not initiated by sunlight.

Ignoring thermochemical reactions is perhaps the most controversial assumption but it is crucial for this paper.

 

Photochemical model

In order to find out how many photons are available at certain depths we will divide the atmosphere into unit cells with a thickness Δp and with a surface area A. In our model of the atmosphere we use pressure instead of height as a vertical coordinate. In physics, weight is a force defined as the product of mass m and gravitational acceleration g and pressure p is the force applied per unit area. The pressure exerted by an air mass therefore depends on the mass of the air and on the area below the mass. The atmosphere changes its composition, density and temperature with depth however since Δ p is constant the mass of air in an atmospheric cell is constant as well. The consequence of that is that all atmospheric cells are of equal size and mutually comparable. We assume that Δ p is sufficiently small that one particle in the cell cannot obscure another particle in the cell. A scheme of such cell is presented in Fig. 3.

Figure 3. Photochemical model of an atmospheric cell. The left part of figure shows the temperature profile for the 'US standard atmosphere' as a function of pressure between 11 km (tropopause) and 84 km altitude (mesopause). In our model of an atmospheric cell S_ac represents the screening of a cell for photons with wavelength λ, N_p(0,λ) the initial amount of photons, N_p(p,λ) the number of photons at depth p and θ is angle between light ray and surface. General characteristics of this model: a) light is made up of particles, b) photons and molecules in the atmospheric cell are homogeneously spread across the surface, c) the atmosphere begins at the source of light - the Sun (p=0), d) pressure is used as a vertical coordinate e) from the viewpoint of the photons molecules in the atmosphere are static, f) photochemical reactions are preferred, g) thermochemical reactions are ignored. → Download high quality image

 

For photons that travel at light speed the molecules in the atmosphere are static (mean speed of N₂ and O₂ molecules in air at 25 °C is about 0.5 km/s). At the moment when it touches the edge of the atmosphere a photon "sees" all particles, atoms and molecules on its path to the surface. The fraction of incident light that is transmitted through a cell depends on the losses that are incurred by absorption, scattering, and luminescence on particles in the cell. By knowing the mass m and composition of air it is easy to calculate the number of molecules of each substance in an atmospheric cell (N_X = w_X·m·L/M_X) where w_X is the mass fraction of a substance X, M_X is the molecular mass of a substance X, and L is Avogadro's number. The probability of a photon hitting a molecule in the cell depends on the ratio of its surface occupied by all molecules (including crude particles). The screening of the atmospheric cell is

Here the absorption cross section σ_X describes the effective area of the molecule X that a photon of wavelength λ needs to traverse in order to be absorbed. Not all particles in an atmospheric cell participate in stopping photons. A part of the particles is located in the shadow created by the cells above it. Hence the contribution of some atmospheric cell to the screening of the atmosphere for light will depend on the transparency of the atmosphere, 1 - S, on the path of the light and the angle θ at which the light rays enter the cell. The screening created by the atmosphere for light of wavelength λ at depth p is

The number of photons of wavelength λ that arrive to an atmospheric cell depends on the number of photons that headed that way, N_p(0,λ) = Eλ/hc, and the transparency of the atmosphere along that path

 

The ozone layer is a statistical creation

The photochemical reactions that can take place depend on the probability that photon will be absorbed by a molecule of X (as measured by the absorption cross section σ_X), the probability that the molecule X will dissociate if absorption occurs (as measured by the quantum yield Φ_X), both as a function of wavelength λ and temperature T, and on the quantity of photons available (actinic flux F). The actinic flux is defined as the radiance integrated over all solid angles. The photolysis frequency J_X (or J-value for short) is an effective first order rate constant for a photochemical reaction of light-absorbing species in the atmosphere.[6]

Ozone is constantly produced and destroyed in a natural cycle. The amount of ozone formed in a unit cell is proportional to the amount of oxygen atoms in it. These oxygen atoms are in small part created through primary production (photolysis of O₂ with photons with λ<240 nm) but the majority are created in the process of photochemical regeneration (λ depends on the species that is being photolysed).

where XO denotes an oxidized species such as O_x, NO_x, HO_x, ClO_x, etc. Despite creating the most oxygen atoms in the mesosphere and stratosphere UV-B radiation is "sterile". It can only recycle oxygen atoms. As time goes by, without primary oxygen atoms the protection against UV radiation becomes weaker and weaker. Oxygen atoms continuously leave the photodissociation cycle through conversion into molecular oxygen by reacting primarily with ozone and nitrogen oxides (N₂O, NO₂), as well as other compounds (H₂O₂, ClO, etc.). Termination of oxygen atoms with man-made chemicals is the place where we should look for man's impact on these processes.

where k_XO is the rate constant for reaction XO + O → X + O₂. When reduced to their basic elements, the transformation of photon energy into heat q can be shown as O₂ + hν → O + O → O₂ + q. If we take temperature as a measure of the energy released in these reactions then the increase of density throughout the whole mesosphere positively affects the efficiency of photon absorption, reaching its maximum in the stratopause. After the stratopause, descending into the depths of the stratosphere is followed by a drop in efficiency of the atmospheric cell (see Fig. 3).

The ozone does not have a shield with which it deflects UV radiation - it sacrifices itself for our protection. Despite all of that, no matter how thick the ozone layer is, it will simply disappear when illuminated. Apart from photolysis ozone can be destroyed by a number of free radicals, the most important of which are atomic oxygen (O), hydroxyl radical (OH), nitric-oxide radical (NO), and atomic chlorine (Cl). By measuring the amounts of ozone in the atmosphere we cannot find out how much ozone was destroyed because the ozone layer represents the "negative image" of the UV radiation protection. We get the ozone layer by summing the residual ozone through the atmospheric column. The residual ozone in each atmospheric cell will be equal to the sum of all screened molecules of ozone that certainly will not dissociate and undissociated molecules on the unscreened part.

Since all photochemical reactions depend only on the probability for them to occur, we can consider the ozone layer a statistical creation.

 

Instead of a Conclusion

The working title of this paper was "Does the Sun's UV radiation protect life on the Earth?" The answer to this question is evident. The question is, are we sabotaging it?

There are a few more questions we need to get answers for before we reach a conclusion:

1. How does depth affect the efficiency of the atmospheric cell in transforming the UV photon energy into the heat (N_O(regenerated) + N_O(primary))?
2. How does the utilization of photons with λ<240 nm in stopping photons with λ<320 nm (N_O(regenerated) / N_O(primary)) change with the change of depth?
3. Does the ratio of resulting oxygen atoms (N_O(regenerated) / N_O(primary)) match the ratio of spent photons (ΔN_p(λ<320 nm) / ΔN_p(λ<240 nm)) in an atmospheric cell?
4. How much does the dissociation of ozone contribute to the number of regenerated oxygen atoms (N_O(reg. from O₃) / N_O(regenerated))?
5. Can the raising of the ozone rich layers to areas where the light can illuminate upon them result in the ozone layer depletion?

 

 

References

1. "Press Release: The 1995 Nobel Prize in Chemistry." Nobel Media AB. 4 Jan. 2015. <http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1995/press.html>
2. Peter Atkins and Julio de Paula. "Physical Chemistry". Oxford University Press. New York. 2002.
3. David R. Williams. "Sun Fact Sheet." 1 July 2013. NASA. 12 Jan. 2015. <http://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html>
4. Eni Generalić. "Black-body radiation calculator." 17 Feb. 2015. <https://www.periodni.com/download/black_body_radiation.xls>
5. "U.S. Standard Atmosphere, 1976." NOAA, NASA and USAF. Washington, D.C. 1976. 15 Jan. 2015. <http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770009539.pdf>
6. Aarnout van Delden. "Atmospheric Dynamics." Utrecht University, Netherlands. 7 Feb. 2015. <http://www.staff.science.uu.nl/~delde102/AtmosphericDynamics.htm>

 

The article "The ozone layer is not a shield, it is the remnant of UV radiation protection" is an open access article distributed under the terms and conditions of the Creative Commons Attribution 4.0 International license (http://creativecommons.org/licenses/by/4.0/).